OPTISIM – Exzellenzcluster PhoenixD – Leibniz Universität Hannover

Unsere Ziele

Das langfristige Ziel von PhoenixD ist die Schaffung einer integrierten Plattform für optische Simulationen, die gemeinsame Nutzung von Daten durch experimentelle und theoretische Gruppen und die Datenverwaltung nach europäischen Protokollen, um die Wiederverwendung von Modellen, Algorithmen und Daten zu ermöglichen. OPTISIM arbeitet gemeinsam an einer Schnittstellenplattform, um die langfristige Vision von PhoenixD zu unterstützen.

Die Plattform wird auf den Bedarf an Forschung und Entwicklung innerhalb von PhoenixD und teilweise auch auf unsere Gemeinschaft weltweit ausgerichtet sein. Sie wird die Modelle, die Theorie, die Funktion, die Struktur und die Schnittstellen der verschiedenen Module in systematischer Weise erklären und darstellen. OPTISIM zielt darauf ab, den hauseigenen Code, kommerzielle Software-Schnittstellen (Lizenzen innerhalb von PhoenixD) und andere Open-Source-Algorithmen für computergestützte Photonik und Optik in einem Rahmen zu integrieren.

Obwohl dies eine ehrgeizige und langfristige Aufgabe ist, besteht unsere erste Phase von OPTISIM darin, den Rahmen zu definieren. Eine solche Plattform muss für die langfristigen Anforderungen in Forschung und Ausbildung eingerichtet und entwickelt werden. Bei der Entwicklung von OPTISIM werden systematische Best Practices des Software-Engineering im Hinblick auf Wartbarkeit, Benutzerfreundlichkeit, Erweiterbarkeit und Übertragbarkeit auf verschiedene Computerplattformen (vom Desktop-Computer bis zum Exascale-Supercomputer) angewendet. Die Struktur von OPTISIM wird die Integration neuer Module unterstützen. Es werden geeignete Datenstrukturen definiert, um den Austausch von Daten zwischen Modulen zu ermöglichen. Diese Software würde die Grundlage für ein virtuelles Labor für das OPTICUM (neues Infrastrukturgebäude auf dem Campus Garbsen) bilden, um komplexe optische Probleme zu simulieren, einschließlich Multiphysik- und Multiskalenszenarien, sowie für den Entwurf und die Optimierung fortgeschrittener photonischer Geräte.

Unsere Forschungsthemen

Multiskalenmodellierung und KI

Bereichsleitung: Prof. Xiaoying Zhuang

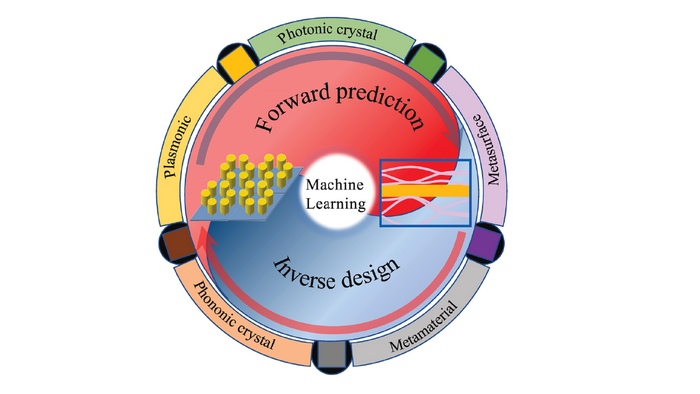
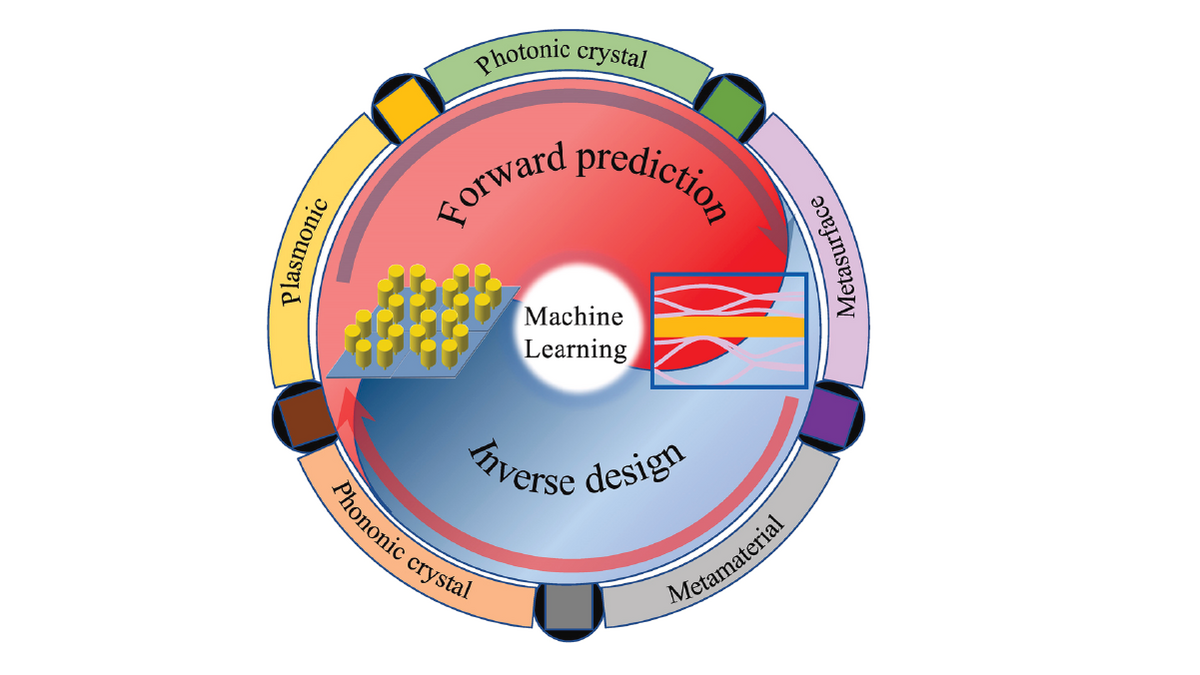
Maschinelles Lernen und rechnergestützte Mechanik für die Modellierung und den Entwurf neuartiger photonischer Systeme, Metamaterialien und Nanostrukturen.

Beispiel: Vielversprechende Photokatalyse in zwei Dimensionen, bestätigt durch erste Prinzipien
Außergewöhnliche Piezoelektrizität, hohe Wärmeleitfähigkeit und Steifigkeit sowie vielversprechende Photokatalyse in der zweidimensionalen MoSi2N4-Familie wurden durch erste Prinzipien bestätigt.

Zum ersten Mal zeigen wir, dass das maschinelle Lernen interatomarer Potenziale, die über kleine Superzellen trainiert wurden, zur Untersuchung der flexoelektrischen und piezoelektrischen Eigenschaften komplexer Strukturen eingesetzt werden kann. Die aufregendste Erkenntnis ist, dass WSi2N4, CrSi2N4 und MoSi2N4 die höchsten piezoelektrischen Koeffizienten aufweisen und alle anderen bekannten 2D-Materialien übertreffen. Unsere Ergebnisse zeigen, dass MA2Z4-Nanoblätter nicht nur die Gruppe der Übergangsmetall-Dichalcogenide zweifellos übertreffen, sondern auch mit Graphen in vielen Anwendungen der Nanoelektronik, Optoelektronik, Energiespeicherung/-umwandlung und Wärmemanagementsystemen konkurrieren können.

Die Originalveröffentlichung ist unter https://doi.org/10.1016/j.nanoen.2020.105716 verfügbar.

Die Arbeit wird vom Team Prof. Xiaoying Zhuang durchgeführt.

Referenz

K.S. Novoselov, A.K. Geim, S. V Morozov, D. Jiang, Y. Zhang, S. V Dubonos, I. V Grigorieva, A.A. Firsov, Electric field effect in atomically thin carbon films., Science. 306 (2004) 666–9.

A.K. Geim, K.S. Novoselov, The rise of graphene, Nat. Mater. 6 (2007) 183–191.
Open-Scource Code: Eine nichtlokale Operator-Methode für Wellenleiterprobleme
Für die Lösung partieller Differentialgleichungen wird eine neuartige nichtlokale Operatortheorie auf der Grundlage des Variationsprinzips vorgeschlagen. Gemeinsame Differentialoperatoren sowie die Variationsformen werden im Zusammenhang mit nichtlokalen Operatoren definiert. Die vorliegende nichtlokale Formulierung ermöglicht die einfache Zusammenstellung der tangentialen Steifigkeitsmatrix, die für die Eigenwertanalyse, z. B. des Wellenleiterproblems, erforderlich ist. Die vorliegende Formulierung wird zur Lösung der differentiellen elektromagnetischen Vektorwellengleichungen auf der Grundlage elektrischer Felder verwendet. Die geltenden Gleichungen werden in eine nichtlokale Integralform umgewandelt. Ein Sanduhr-Energiefunktional wird für die Eliminierung von Null-Energie-Moden eingeführt. Schließlich wird die vorgeschlagene Methode durch die Prüfung von drei klassischen Benchmark-Problemen validiert.

Die Originalveröffentlichung ist unter https://doi.org/10.32604/cmc.2019.04567 verfügbar.

Die Arbeit wurde von dem Team Prof. Xiaoying Zhuang durchgeführt.

Referenz

Kamensky, David, et al. Immersogeometric cardiovascular fluid–structure interaction analysis with divergence-conforming B-splines. Computer methods in applied mechanics and engineering 314 (2017): 408-472.

Ren, Huilong, Xiaoying Zhuang, and Timon Rabczuk. Dual-horizon peridynamics: A stable solution to varying horizons. Computer Methods in Applied Mechanics and Engineering 318 (2017): 762-782.

Wissenschaftliches Rechnen bei nichtlinearen gekoppelten Problemen in der Optik

Bereichsleitung: Prof. Thomas Wick

Mathematische Modellierung, adaptive Diskretisierung und effiziente numerische Lösungen von nichtlinearen und linearen Problemen in optischen Systemen.

Open-Source-Code: Parallele Domänenzerlegungslöser für die zeitharmonischen Maxwell-Gleichungen

Die zeitharmonischen Maxwell-Gleichungen (THM) sind von großem Interesse für die angewandte Mathematik und aktuelle physikalische Anwendungen, z. B. für den Exzellenzcluster PhoenixD. Allerdings ist die numerische Lösung eine Herausforderung. Dies gilt insbesondere für hohe Wellenzahlen. Es wurden verschiedene Löser und Vorkonditionierer vorgeschlagen, wobei die vielversprechendsten auf Domänenzerlegungsmethoden (DDM) beruhen.

Das Ziel dieser Arbeit ist es, eine Domänenzerlegungsmethode zu verwenden und den Algorithmus in der modernen Finite-Elemente-Bibliothek deal.II neu zu implementieren. Dabei ist die Konstruktion der Randbedingungen für das Teilgebiet ein entscheidender Aspekt, für den wir Impedance Boundary Conditions verwenden. Anstatt das resultierende lineare System mit einem direkten Löser zu behandeln, wie es typischerweise für die THM gemacht wird, wenden wir einen gut gewählten Block-Vorkonditionierer auf das lineare System an, so dass wir es mit einem iterativen Löser wie GMRES (generalized minimal residuals) lösen können. Zusätzlich werden hochpolynomielle Nédélec-Elemente bei der Implementierung des DDM verwendet. Diese Implementierung wird rechnerisch mit mehreren anderen (klassischen) Vorkonditionierern wie unvollständiger LU, additiver Schwarz, Schur-Komplement verglichen. Diese Vergleiche werden für verschiedene Wellenzahlen durchgeführt. Höhere Wellenzahlen stellen bekanntermaßen eine Herausforderung für die numerische Lösung dar.

Die Originalveröffentlichung ist unter https://link.springer.com/chapter/10.1007/978-3-030-95025-5_71 verfügbar.

Lesen Sie mehr und laden Sie den Code hier herunter: https://github.com/tommeswick ; https://github.com/kinnewig

Die Arbeit wird von S. Beuchler, S. Kinnewig und T. Wick innerhalb des Teams von Prof. Thomas Wick durchgeführt.
Open-Scource Code: Algorithmische Realisierung der Lösung des Vorzeichenkonfliktproblems für hängende Knoten auf hp-hexaedrischen Nédélec-Elementen

Bei der Arbeit mit Nédélec-Elementen auf adaptiv verfeinerten Netzen mit hängenden Knoten muss die Orientierung der hängenden Kanten und Flächen berücksichtigt werden. Für nicht orientierbare Netze gab es bisher keine Lösung und Implementierung. Die Problemstellung und die entsprechenden Algorithmen werden sehr detailliert beschrieben. Als Modellproblem werden die zeitharmonischen Maxwell-Gleichungen gewählt, da Nédélec-Elemente deren natürliche Diskretisierung darstellen. Die Implementierung erfolgt mit der Finite-Elemente-Bibliothek deal.II. Die Algorithmen und die Implementierung werden anhand von vier numerischen Beispielen auf verschiedenen gleichmäßig und adaptiv verfeinerten Netzen demonstriert.

Die Originalveröffentlichung ist unter https://arxiv.org/abs/2306.01416 verfügbar.

Lesen Sie mehr und laden Sie den Code von hier herunter: https://github.com/tommeswick, https://github.com/kinnewig

Die Arbeit wird von S. Kinnewig, T. Wick, S. Beuchler innerhalb des Teams von Prof. Thomas Wick durchgeführt.

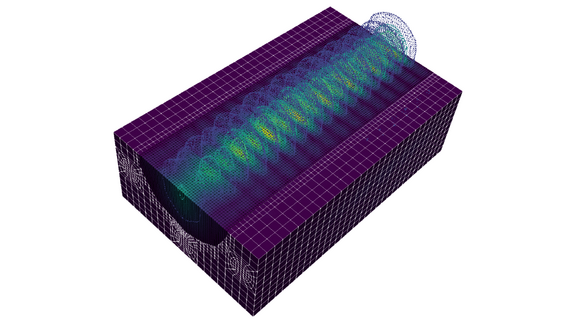
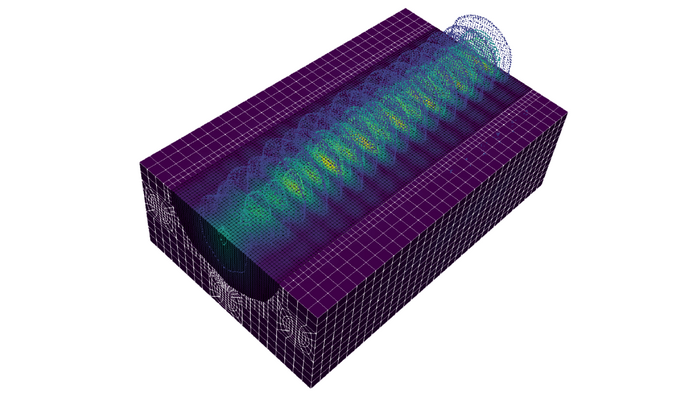
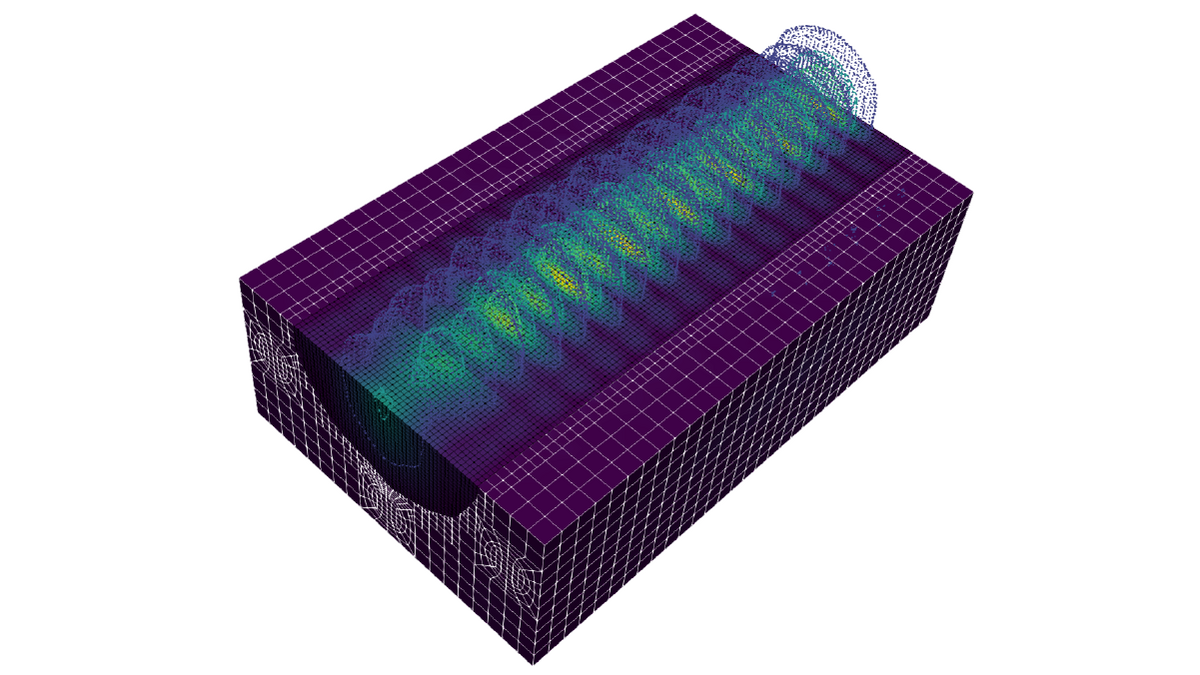
Computational Nonlinear Optics

Bereichsleitung: Prof. Ayhan Demircan

Theoretische und rechnerische Untersuchungen von Multiphysik- und Multiskalenproblemen in nichtlinearen optischen Systemen.

Open-Source Code: Ein verallgemeinertes nichtlineares Schrödinger-Python-Modul, das verschiedene Modelle von Eingangsimpuls-Quantenrauschen implementiert
Wir stellen Python-Tools zur Verfügung, die eine numerische Simulation und Analyse der Ausbreitungsdynamik ultrakurzer Laserpulse in nichtlinearen Wellenleitern ermöglichen. Der Modellierungsansatz basiert auf der weit verbreiteten verallgemeinerten nichtlinearen Schrödinger-Gleichung für die Pulshülle. Die mitgelieferte Software implementiert die Effekte der linearen Dispersion, der Pulsselbstvertiefung und des Raman-Effekts. Der Schwerpunkt liegt auf der Implementierung von Eingangsimpuls-Schussrauschen, d.h. klassischen Hintergrundfeldern, die Quantenrauschen imitieren, das in der wissenschaftlichen Literatur oft nicht ausführlich dargestellt wird. Wir diskutieren und implementieren gängige Quantenrauschmodelle, die auf reinem spektralen Phasenrauschen sowie auf Gaußschem Rauschen basieren. Die Kohärenz-Eigenschaften der resultierenden Spektren können berechnet werden. Wir demonstrieren die Funktionalität der Software durch die Reproduktion von Ergebnissen für einen Superkontinuum-Erzeugungsprozess in einer photonischen Kristallfaser, die in der wissenschaftlichen Literatur dokumentiert sind. Die vorgestellten Python-Tools sind Open-Source und werden unter der MIT-Lizenz in einem öffentlich zugänglichen Software-Repository veröffentlicht.

Plattform: Python, unter Verwendung der Funktionen von numpy, scipy und matplotlib.

Lesen Sie mehr und laden Sie den Code von hier herunter:
https://github.com/ElsevierSoftwareX/SOFTX-D-22-00165.git

Wir haben eine Code Ocean-Kapsel vorbereitet, die es ermöglicht, eine Beispielsimulation direkt auszuführen und zu verändern, ohne eine lokale Kopie des Repositorys unter dem Link erstellen zu müssen: https://codeocean.com/capsule/4658074/tree

Die Arbeit wird von dem Team von Prof. Ayhan Demircan durchgeführt.

Referenz

Melchert, Oliver and Demircan, Ayhan. GNLStools.py: A generalized nonlinear Schrödinger Python module implementing different models of input pulse quantum noise. SoftwareX 20 (2022): 101232.

Melchert, Oliver et al. Soliton compression and supercontinuum spectra in nonlinear diamond photonics. Diamond & Related Materials 136 (2023): 109939.
Open-Scource Code: Ein Python-Paket für ultrakurze optische Pulsausbreitung in Form von Vorwärtsmodellen für das analytische Signal
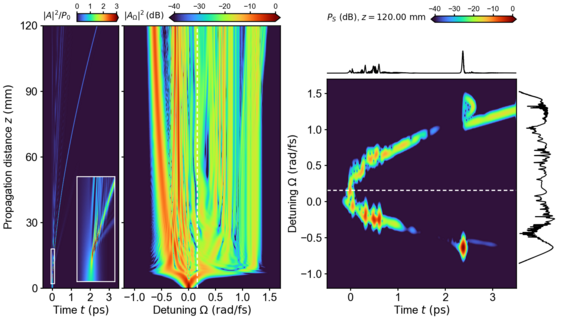
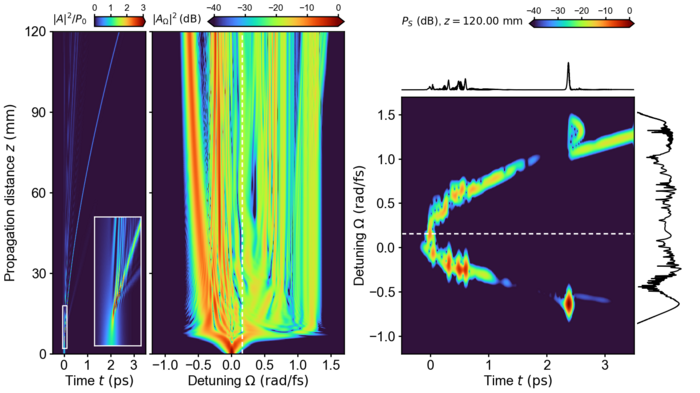
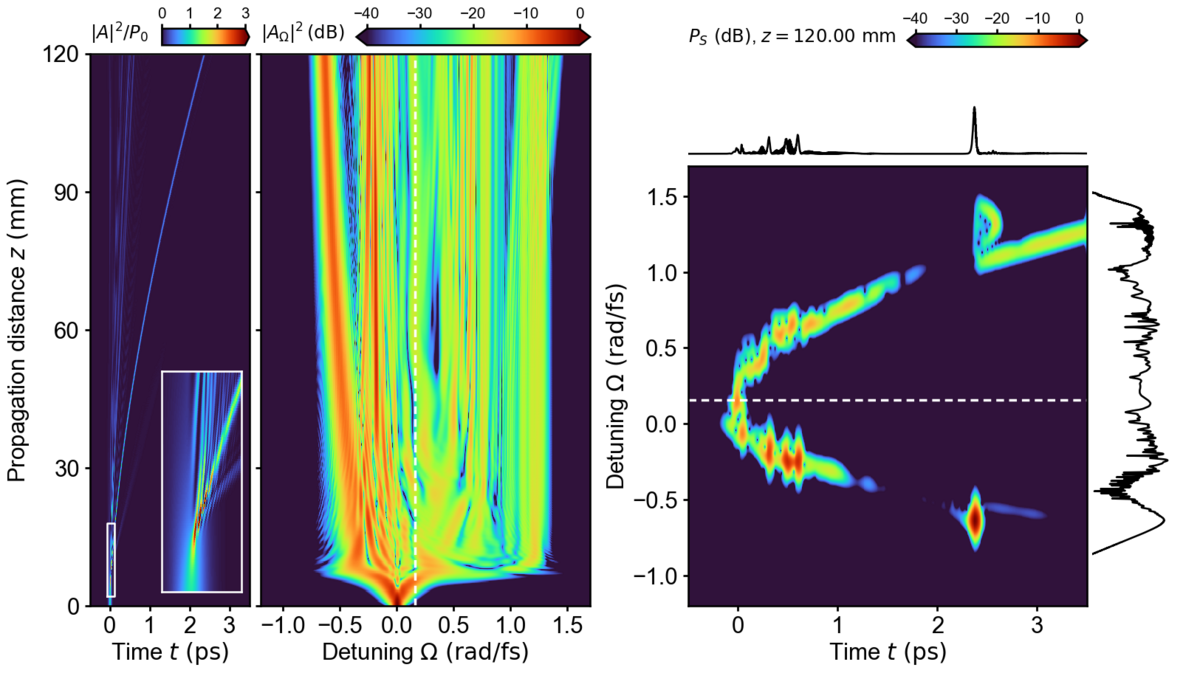
Wir stellen ein flexibles, quelloffenes Python-Paket für die genaue Simulation der z-Ausbreitungsdynamik ultrakurzer optischer Pulse in nichtlinearen Wellenleitern vor, das insbesondere für Pulse mit wenigen Zyklen und deren Wechselwirkung gilt. Der Simulationsansatz basiert auf unidirektionalen Ausbreitungsgleichungen für das analytische Signal. Die mitgelieferte Software ermöglicht die Berücksichtigung von Dispersion, Dämpfung und Vier-Wellen-Mischungsprozessen, einschließlich z.B. der Erzeugung der dritten Harmonischen, und bietet verschiedene Modelle für die Raman-Antwort. Die Ausbreitungsgleichungen werden in einem periodischen Zeitbereich gelöst. Für die z-Ausbreitung steht eine Auswahl an pseudospektralen Methoden zur Verfügung. Ausbreitungsszenarien für eine benutzerdefinierte Ausbreitungskonstante und anfängliche Feldimpulse können entweder in Form eines HDF5-basierten Eingabedateiformats oder durch direkte Implementierung mit einem Python-Skript angegeben werden. Wir demonstrieren die Funktionalität für einen Testfall, für den eine exakte Lösung verfügbar ist, indem wir beispielhafte, in der wissenschaftlichen Literatur dokumentierte Ergebnisse reproduzieren, sowie für ein komplexes Ausbreitungsszenario mit mehreren Impulsen.

Lesen Sie mehr und laden Sie den Code von hier herunter: https://data.mendeley.com/datasets/7s2cv9kjfs/1

Wir haben eine Code Ocean-Kapsel vorbereitet, die es ermöglicht, eine Beispielsimulation direkt auszuführen und zu ändern, ohne eine lokale Kopie des Repositorys unter dem Link erstellen zu müssen: https://codeocean.com/capsule/4971866/tree

Die Arbeit wird von dem Team von Prof. Ayhan Demircan durchgeführt.

Referenz

Melchert, Oliver and Demircan, Ayhan. py-fmas: A python package for ultrashort optical pulse propagation in terms of forward models for the analytic signal. Computer Physics Communications 273(2022): 108257.

Melchert, Oliver et al. Resonant Kushi-comb-like multi-frequency radiation of oscillating two-color soliton molecules. New J. Phys. 25 (2023): 013003.

Melchert, Oliver et al. (Invited) Two-color soliton meta-atoms and molecules. Optik 280 (2023): 170772.

Melchert, Oliver and Demircan, Ayhan. Two-color pulse compounds in waveguides with a zero-nonlinearity point. Opt. Lett. 48 (2023): 518.
Open-Scource Code: Ein Python-Toolkit zum Lösen der verallgemeinerten Lugiato-Lefever-Gleichung
Wir stellen ein Python-Toolkit zur Simulation der Ausbreitungsdynamik von dissipativen Solitonen in einer Variante der Lugiato-Lefever-Gleichung (LLE) vor, die Dispersionsterme dritter und vierter Ordnung enthält. Darüber hinaus ermöglicht die Software die Vorbereitung von Anfangsbedingungen, die durch stationäre lokalisierte Lösungen der Standard-LLE im anomalen Gruppengeschwindigkeits-Dispersionsbereich gegeben sind. Ausbreitungsszenarien für benutzerdefinierte Kontrollparameter und Anfangsbedingungen können vom Benutzer über eine einfache Klassendatenstruktur festgelegt werden. Wir demonstrieren die implementierte Funktionalität, indem wir zeigen, wie man stationäre Lösungen der Standard-LLE erhält, die ein dissipatives Soliton enthalten, und indem wir verschiedene charakteristische Ausbreitungsszenarien demonstrieren. Das pyGLLE-Softwarepaket ist Open-Source und wird unter der X11-Lizenz in einem öffentlich zugänglichen Software-Repository veröffentlicht.

Plattform: Python, unter Verwendung der Funktionen von numpy, scipy und matplotlib.

Lesen Sie mehr und laden Sie den Code von hier herunter: https://github.com/ElsevierSoftwareX/SOFTX_2020_88

Wir haben eine Code Ocean-Kapsel vorbereitet, die es ermöglicht, eine Beispielsimulation direkt auszuführen und zu verändern, ohne eine lokale Kopie des Repositorys unter dem Link erstellen zu müssen: https://codeocean.com/capsule/9315811/tree/

Die Arbeit wird von dem Team von Prof. Ayhan Demircan durchgeführt.

Referenz

Melchert, Oliver and Demircan, Ayhan. pyGLLE: A Python toolkit for solving the generalized Lugiato–Lefever equation. SoftwareX 15 (2021): 100741.

Melchert, Oliver and Demircan, Ayhan and Yulin, Alexey. Multi-frequency radiation of dissipative solitons in optical fiber cavities. Scientific Reports 10 (2020): 8849.

Melchert, Oliver and Yulin, Alexey and Demircan, Ayhan. Dynamics of localized dissipative structures in a generalized Lugiato–Lefever model with negative quartic group-velocity dispersion. Opt. Lett. 45 (2020): 2764.
Open-Scource Code: Analytische Signalspektrogramme mit optimierter Zeit-/Frequenzauflösung

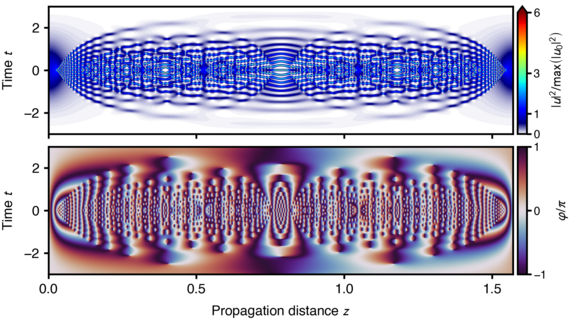
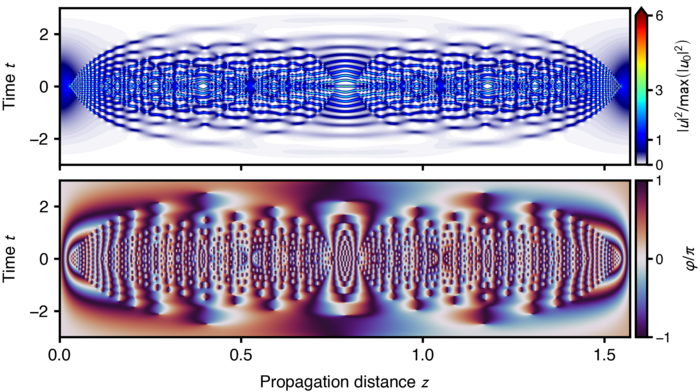
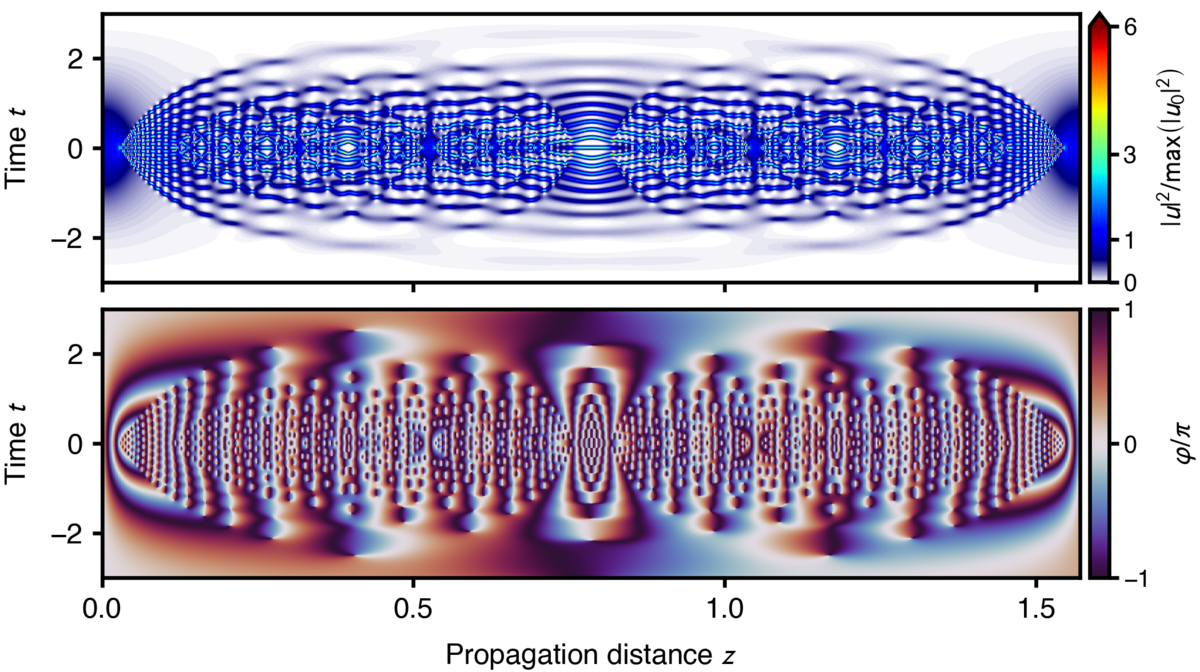
Es wird ein Python-Paket zur Berechnung von Spektrogrammen mit optimierter Zeit- und Frequenzauflösung für die Analyse von numerischen Simulationen zur Ausbreitung ultrakurzer Impulse vorgestellt. Das Gaborsche Unschärfeprinzip verhindert, dass beide Auflösungen für eine gegebene Fensterfunktion, die in der zugrunde liegenden Kurzzeit-Fourier-Analyse verwendet wird, gleichzeitig optimal sind. Unser Ziel ist es, eine Zeit-Frequenz-Darstellung des Eingangssignals mit Randwerten zu erhalten, die die ursprünglichen Intensitäten pro Zeit- und Frequenzeinheit ähnlich gut darstellen. Als Anwendungsfall demonstrieren wir die implementierte Funktionalität für die Analyse von Simulationen zur Ausbreitung ultrakurzer Impulse in einem nichtlinearen Wellenleiter.

Plattform: Python, unter Verwendung der Funktionen von numpy, scipy und matplotlib.

Lesen Sie mehr und laden Sie den Code von hier herunter: https://github.com/ElsevierSoftwareX/SOFTX_2019_130

Wir haben eine Code Ocean-Kapsel vorbereitet, die es ermöglicht, eine Beispielsimulation direkt auszuführen und zu verändern, ohne eine lokale Kopie des Repositorys unter dem Link erstellen zu müssen: https://codeocean.com/capsule/7823161/tree

Die Arbeit wird von dem Team von Prof. Ayhan Demircan durchgeführt.

Referenz

Melchert, Oliver and Roth, Bernhard and Morgner, Uwe and Demircan, Ayhan. OptFROG — Analytic signal spectrograms with optimized time–frequency resolution. SoftwareX 10 (2019): 100275.

Unsere Kompetenzen im Team

Forschungsbereich - Multiskalenmodellierung und KI

Das Hauptforschungsgebiet von Prof. Xiaoying Zhuang ist maschinelles Lernen und Computermechanik für die Modellierung und das Design neuartiger photonischer Systeme, Metamaterialien und Nanostrukturen. Sie hat zahlreiche innovative und robuste numerische Methoden entwickelt, darunter Level-Set-Methoden, Partition-of-Unity-Methoden (wie netzfreie Methoden, XFEM-Formulierungen, Phantomknoten-Methoden und Finite-Cover-Methoden), Multiskalen-Methoden, Phasenfeldmodelle und fehlergesteuerte adaptive Methoden, die sie entwickelt und umgesetzt hat. Sie hat auch Erfahrung mit gekoppelten (hydro-mechanischen, thermo-mechanischen, thermo-hydro-mechanischen und elektro-mechanischen) Problemen, Unsicherheitsanalysen/Unsicherheitsquantifizierung sowie inversen Methoden und Optimierungsverfahren. Sie hat innovative numerische Methoden angewandt, um komplexe Probleme in den Bereichen Ingenieurwesen, Festkörperphysik und Materialwissenschaften zu lösen. Der Forschungsschwerpunkt des von der Humboldt-Stiftung geförderten Projekts von Sofja Kovalevskaja ist die Modellierung, Optimierung und Entwicklung von Polymerverbundwerkstoffen. Ihr laufender ERC Starting Grant konzentriert sich auf die Optimierung und Entwicklung von piezoelektrischen und flexoelektrischen Nano-Energiewandlern.

Prof. Xiaoying Zhuang

Forschungsbereich - Computergestützte nichtlineare Optik

Die Forschungsaktivitäten der Gruppe befassen sich mit der theoretischen Untersuchung komplexer Dynamiken, die in nichtlinearen Systemen in verschiedenen Bereichen auftreten. Zu diesen Bereichen gehören die moderne nichtlineare Optik, die Quantenoptik, die Materialwissenschaften und die Physik der kondensierten Materie, aber auch die Strömungsdynamik und verwandte Gebiete. Die Untersuchungen umfassen die theoretische Analyse der grundlegenden Effekte, die Modellierung sowie die Entwicklung und Anwendung geeigneter numerischer Methoden. Es wird eine breite Palette von Methoden entwickelt und angewandt, die von spektralen und statistischen Methoden bis hin zu Finite-Differenzen-Zeitbereichsverfahren reichen. Unsere Aktivitäten lassen sich in drei Hauptkategorien unterteilen: Methodenentwicklung, nichtlineare Wellenwechselwirkung und Solitonenphysik sowie nichtlineare Photonik kondensierter Materie.

Prof. Ayhan Demircan

Forschungsgebiet - Wissenschaftliches Rechnen bei nichtlinearen gekoppelten Problemen in der Optik

Prof. Thomas Wicks Forschungsinteressen sind der Entwurf, die Implementierung und die Analyse numerischer Algorithmen und Raum-Zeit-Methoden für nichtstationäre, nichtlineare, gekoppelte PDE-Systeme und Variationsungleichungen in den Bereichen Strömungsdynamik, Festkörpermechanik, Fluid-Struktur-Wechselwirkung, Thermoporelastizität und Rissausbreitungsprobleme in Elastizität und Poroelastizität. Dabei interessiert er sich insbesondere für nichtlineare Löser, a posteriori-Fehlerabschätzung, adaptive Methoden wie lokale Netzadaptivität mit besonderem Schwerpunkt auf zielorientierten Techniken unter Verwendung von Adjunkten und parallelem Hochleistungsrechnen. Diese Konzepte werden darüber hinaus in der numerischen Optimierung für optimale Steuerung, optimales Design und Parameterschätzung eingesetzt. Ein wichtiger Teil der Arbeit der Gruppe von Prof. Wick befasst sich mit der nachhaltigen, modernen Entwicklung von Forschungssoftware.